| OptiLayer enables you to specify integral target characteristics and optimize a design with respect to these characteristics. Integral targets are used, when averaged/integral values of a design should takes specified values.
In OptiLayer, integral targets are represented as finite sums and can be considered as approximations of an integral expression with the help of rectangle rule. As in conventional targets it is possible to specify
|
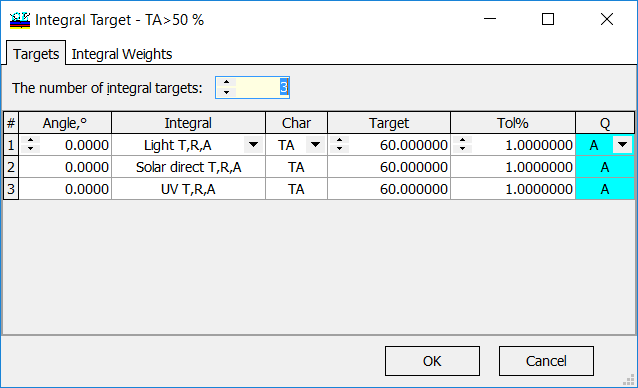
Fig. 1. Specification of integral target. The integral target window consists of Targets and Integral Weights panels. In the example (Fig. 1), transmittance (TA, no polarization) is integrated with three commonly used spectral weight functions. It is required that the integral values are to be more than 60%. |
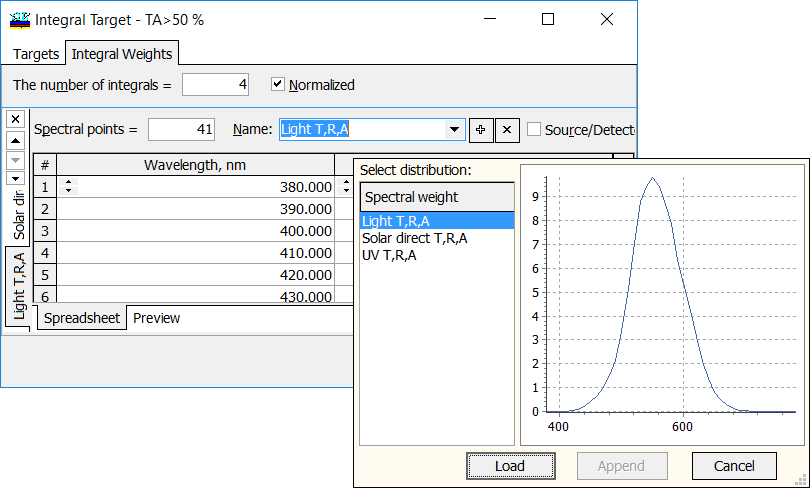
Fig. 2. Spectral distributions of the target weights can be chosen from a pop-up list in the Integral Weights tab. |
In order to specify the Integral type (Integral), you should choose corresponding Integral Weights spectral dependencies.
There are three predefined commonly used spectral weights distributions: Light T,R,A – normalized relative spectral distribution of illuminant D65 multiplied by the spectral luminous efficiency. Solar direct T,R,A – normalized relative spectral distribution of global solar radiation. UV T,R,A – normalized relative spectral distribution of the UV part of the global solar radiation. |
| Spectral distributions of the integral weights can be plotted using Preview panel of the Integral Weights tab.
Switching between different distributions on the left panel, you can observe different spectral weights distributions. Up to 128 different spectral weight functions \(W(\lambda)\) can be defined and used in OptiLayer. |
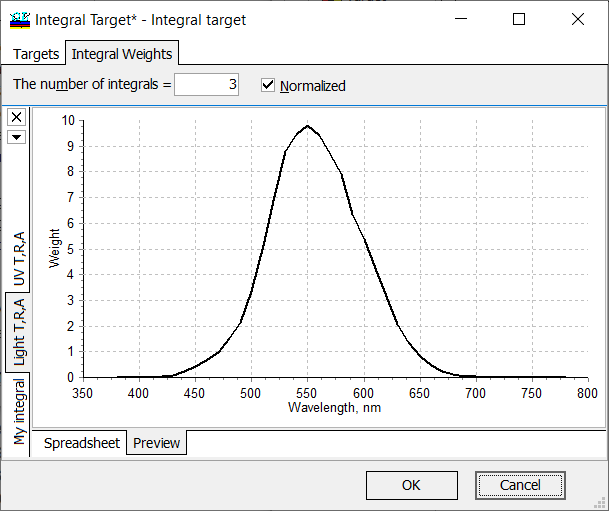
Fig. 3. Spectral distributions of the target weights are plotted in Preview panel of the Integral Weight tab. |
Along with the predefined spectral distribution of the integral weight, it is possible to specify and load your own spectral distributions. The corresponding weight function \(W(\lambda)\) is to be specified at some wavelength grid. It can done:
Fig. 4. Example of user-defined integral weights. |
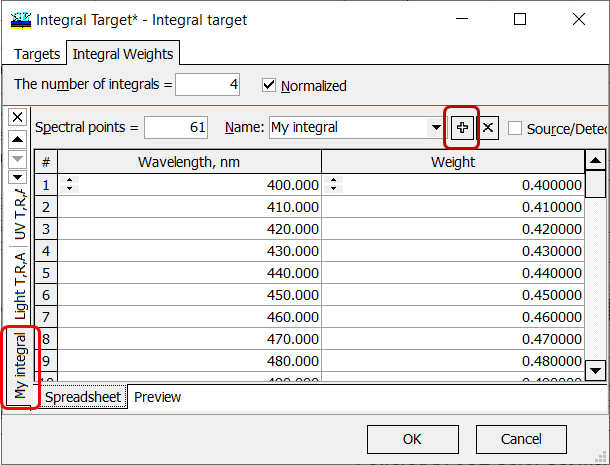
Fig. 5. Adding “My integral” to the available integrals. |
| If you would like to specify not integral but an averaged value (averaged over a spectral range), you can add new Integral Weights spreadsheets (Fig. 5). By default a spreadsheet containing unit values only will be created. You can set the number of spectral points and the spectral range.
Default names are F1, F2, etc. Of course, you can rename the distributions for your convenience. Specifying this unit function in Integral Target window (Fig. 1), you will get averaged values in the specified spectral range over the specified number of spectral points. |
Final expression for the term corresponding to the integral target in the merit function looks as follows:
\[ MF_{int}^2=\frac 1M\sum\limits_{i=1}M\left[\frac{F^{(i)}-\hat{F}^{(i)}}{\Delta F^{(i)}}\right]^2, \] where \(M\) is the number of different integrals in the resulting target (Fig. 1), \(F^{(i)}\) are target values, \(\Delta F^{(i)}\) are corresponding tolerances (Fig. 1). |
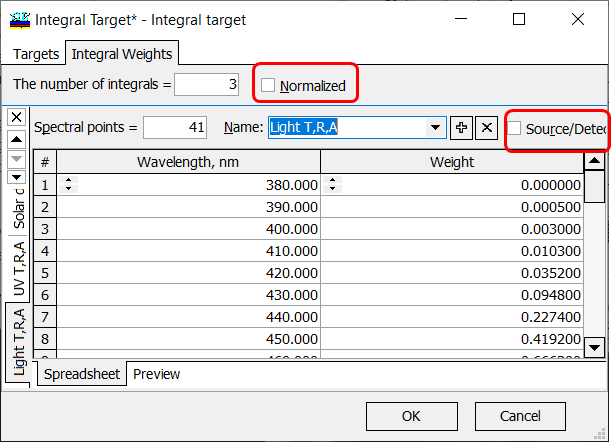
Fig. 6. Normalized and Source/Data check boxes are unchecked. |
If Normalized and Source/Data check boxes are unchecked (Fig. 6), OptiLayer calculates an integral characteristic \(F\) has the form:
\[ F=\int\limits_{\lambda_d}^{\lambda_u} W(\lambda) C(\lambda)d\lambda,\] where \(\lambda_d\) and \(\lambda_u\) are boundaries of the wavelength interval of interest, \(W(\lambda)\) is a given weight function, \(C(\lambda)\) is a spectral characteristic of the coating. |
| If your integral characteristic should be normalized with respect to the spectral distribution of integral weights, then Normalized check box should be checked. In this case:
\[ F=\frac{\int\limits_{\lambda_d}^{\lambda_u} W(\lambda)C(\lambda)d\lambda}{\int\limits_{\lambda_d}^{\lambda_u} W(\lambda) d\lambda},\] where \(\lambda_d\) and \(\lambda_u\) are boundaries of the wavelength interval of interest, \(W(\lambda)\) is a given weight function, \(C(\lambda)\) is a spectral characteristic of a coating. |
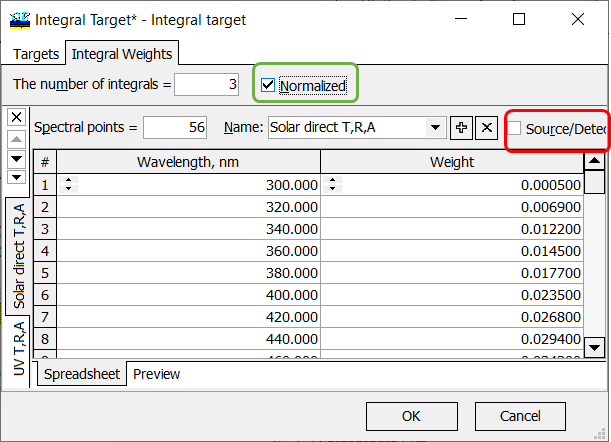
Fig. 7. An integral characteristic will be normalized with respect to the target weights, source and detector are not taken into account. |
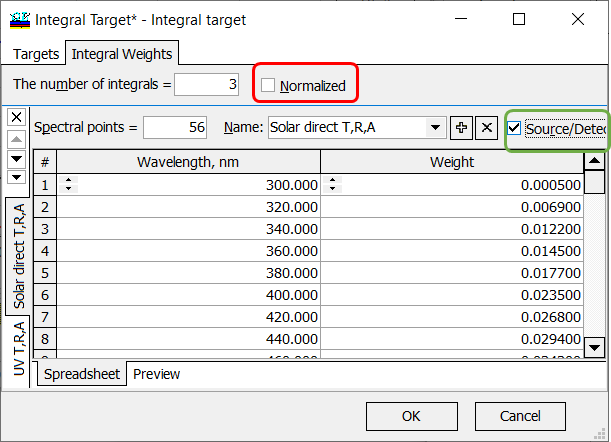
Fig. 8. An integral characteristic will be not normalized with respect to the target weights, source and detector are taken into account. |
If your integral characteristic should take spectral distribution of source/detector into account, then Source/Detector check box should be checked. If your integral characteristic should not be normalized with respect to the spectral distribution of integral weights, then Normalized check box should be unchecked. In this case:
\[ F=\int\limits_{\lambda_d}^{\lambda_u} W(\lambda)D(\lambda) S(\lambda) C(\lambda)d\lambda,\] where \(\lambda_d\) and \(\lambda_u\) are boundaries of the wavelength interval of interest, \(W(\lambda)\) is a given weight function, \(C(\lambda)\) is a spectral characteristic of a coating, \(D(\lambda)\) and \(S(\lambda)\) are spectral distributions of the detector and light source, respectively. |
| If your integral characteristic should take spectral distribution of source/detector into account and If your integral characteristic should not be normalized with respect to the spectral distribution of integral weights, then both check boxes Source/Detector and Normalized are to be checked. In this case:
\[ F=\frac{\int\limits_{\lambda_d}^{\lambda_u} W(\lambda)D(\lambda) S(\lambda) C(\lambda)d\lambda}{\int\limits_{\lambda_d}^{\lambda_u} W(\lambda) S(\lambda) D(\lambda)d\lambda},\] where \(\lambda_d\) and \(\lambda_u\) are boundaries of the wavelength interval of interest, \(W(\lambda)\) is a given weight function, \(S(\lambda)\) is a spectral characteristic of a coating, \(D(\lambda)\) and \(S(\lambda)\) are spectral distributions of the detector and light source, respectively. |
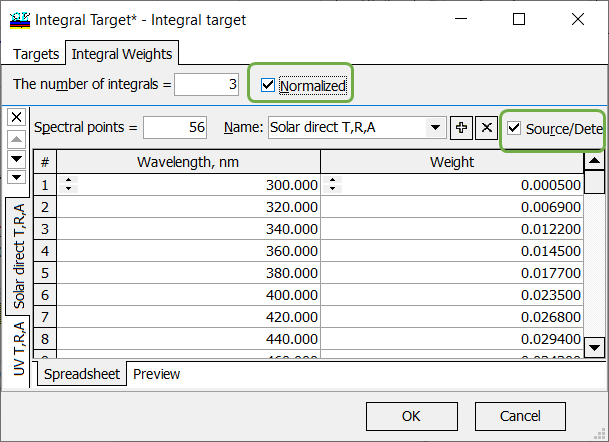
Fig. 9. An integral characteristic will be normalized with respect to the target weights, source and detector are taken into account. |
Look our video examples at YouTube
OptiLayer videos are available here:
Overview of Design/Analysis options of OptiLayer and overview of Characterization/Reverse Engineering options.
The videos were presented at the joint Agilent/OptiLayer webinar.